3个旋转向量算法的比较
1. 旋转算法
《CSAPP》看到《存储器层次结构》的时候,突然醒悟暑假时看《编程珠玑》的一个疑惑。题目是这样的:
写出算法将一个n元一维向量左旋转i个位置。
例如,当n=8且i=3时,向量abcdefgh旋转为defghabc。
《编程珠玑》上给出了5种算法(我就不逐一说明了),下面是这里要讨论的3种:
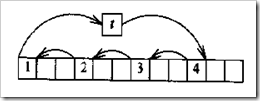
杂技算法
移动x[0]到临时变量t,然后移动x[i]至x[0],x[2i]至x[i](x的下标对n取模),以此类推,直至返回到取x[0]中的元素,此时改为从t中取值并终止程序。若该过程没有移动全部元素,就从x[1]开始再次移动,直到所有元素都已经移动为止。示意图如下:
块交换算法
旋转向量
x是交换向量ab的两段,得到向量ba(这里a代表x中的前i个元素)。假设a比b短,将b分为b1和b2,使得b2具有与a相同的长度。交换a和b2,也就将ab1b2转换为b2b1a。序列a此时已处于其最终的位置,因此问题转换为交换b的两部分,而此问题与原问题形式相同。求逆算法
对
a求逆,对b求逆,再对整体求逆。示意图如下: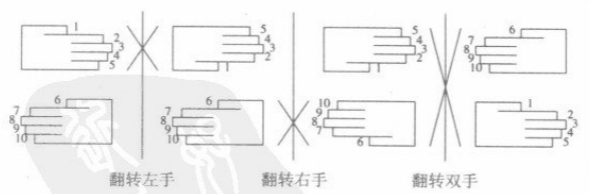
杂技算法的运行速度理论上是求逆算法的两倍,因为杂技算法对数组的每个元素仅存储和读取一次,而求逆算法需要两次。但在实际试验时出现了令我震惊的结论。
习题答案中,作者在400MHz的Pentium机器上运行了杂技算法、求逆算法和快交换算法。运行时把n固定为1000000,并使旋转距离从1变化到50。下图绘制了在每个数据集上50次运行的平均时间:
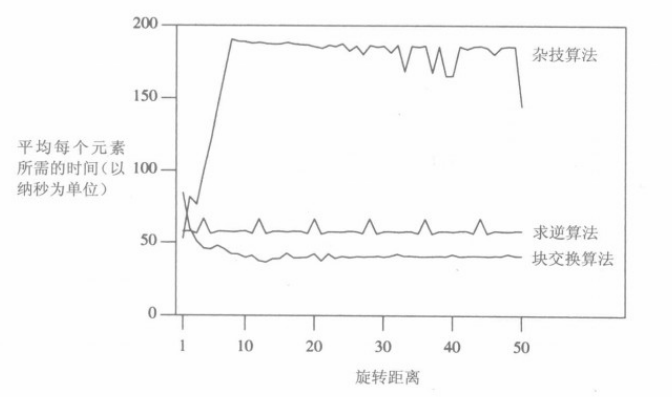
从图中我们可以得到以下结论:
- 块交换算法(作为一个没有引起我注意的算法)在i>2时,是这三个算法中最快的算法。
- 杂技算法的单位开销是求逆算法的三倍以上,也就是说杂技算法的总体时间开销是求逆算法的1.5倍以上。(杂技算法比求逆算法要慢!)
《编程珠玑》上说块交换算法有良好的高速缓存性能,而杂技算法的高速缓存性能差。但我不是很理解高速缓存的意思,网上也没有一个能让我看懂的解释。(这说明《CSAPP》还是厉害( ̄▽ ̄)”)
2. 高速缓存
高速缓存是一个小而快速的存储设备,它作为存储再更大、更慢的设备中的数据对象的缓冲区域。使用高速缓存的过程称为缓存。
存储器层次结构是高速缓存的抽象。
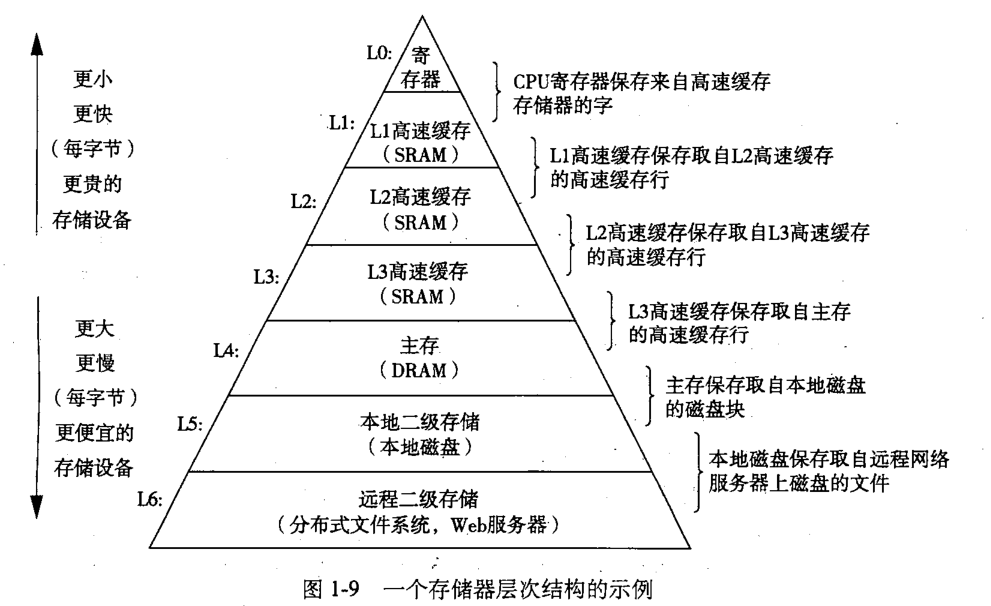
在存储器层次结构中,对于每个k,位于k层的更快更小的存储设备会作为位于k+1层的更大更慢的存储设备的缓存(也就是为其备份数据,让数据更快被读取)。
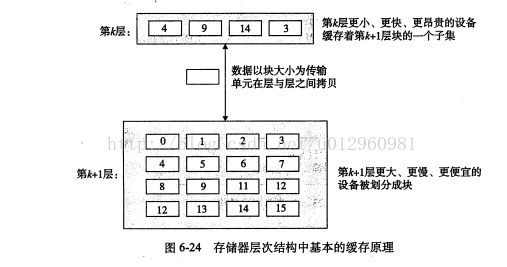
上图展示了存储器层次结构中缓存的一般性概念。第k+1层的存储器被划分成连续的数据对象片,称为块。每个块都有一个唯一的地址(名字)使其区别于其他块。类似地。第k层的存储器也被划分成较小的块的集合,每个块的大小与k+1层的块大小相同。在任一时刻,第k层的缓存都包含第k+1层块的一个子集拷贝。数据总是以块的形式在第k层和第k+1层之间来回拷贝。
虽然在层次结构中任何一对相邻的层次之间块大小是固定的,但其他层次对之间的块大小可以不同。一般而言,较低层的结构因访问速度慢更倾向于使用较大的块。
由于存储器层次结构以块的方式进行缓存,为了适应这一结构,我们在实际编程中应该编写具有良好“局部性”的程序。
局部性通常分为两种不同的形式:时间局部性和空间局部性。在具有良好的时间局部性程序中,被引用过一次的存储器位置很可能在不远的将来再被多次引用(即使用同一个变量);在具有良好的空间局部性程序中,如果存储器位置被引用了一次,那么程序很可能在不远的将来引用附近的一个存储器的位置(即使用数组并低维度优先邻近引用)。
int sum(int a[n][m])
{
int sum = 0, i, j;
for (i = 0; i < n; i++)
for (j = 0; i < m; j++)
sum += a[i][j];
return sum;
}
我们说变量sum使函数具有了良好的是时间局部性;数组通过行优先访问(步长为1)的引用模式使函数具有了良好的空间局部性。若循环变成下面这样:
for (i = 0; i < m; i++)
for (j = 0; j < n; j++)
sum += a[j][i];
我们则说它不具备良好的空间局部性,因为数组通过列优先访问(步长为m)。
3. 结论
那么不难看出高速缓存性能好其实是在说“程序具有良好的局部性”。
现在我们回过头看那三个算法:
- 同:
- 三个算法的时间复杂度相同,都是O(n)。
- 异:
- 块交换算法是以局部性为基础思考的一个算法。虽然它的读写次数最多,但由于其高速缓存性能好,导致读写速度快,成为在i>2时效率最高的算法。
- 求逆算法由于求逆数据块较大,完整的缓存块理论上处于比块交换算法低的位置,所以读取效率比块交换稍慢。
- 杂技算法的步长为2m,导致缓存命中率低(高速缓存性能差),读写速度慢,成为三个算法中效率最慢的算法。